
题目分析
这个题目看上去非常复杂,题目意思是每次获得牌的点数为1-W之间,大于等于K则不再要牌,否则继续要牌,如果手中牌的点数之和小于等于N则赢,求赢的概率。
DFS
最直观的想法,深度搜索,第一张牌有w种抽法,第二张牌有w种抽法,如果最后值大于N,则不加入获胜总概率,如果最后值大于等于K小于N则加入获胜总概率。时间复杂度较高。但是利用python常用库functools中的lru_cache,可以大大节约计算量,会保存计算过的值,如dfs(20, 0.001)已经计算过了,则会建立一个字典,保存这个值,再次调用时会直接获取字典中的值,避免了重复计算。
1 | from functools import lru_cache |
BFS
可以使用DFS的题目一般都可以使用BFS来求解,思路也比较清晰,抽取第一张牌有W中可能,将这些可能的结果都保存在双端队列中,然后抽取第二张牌,将第二张牌所有可能的结果都保存到双端队列中,如果最后值大于N,则不加入获胜总概率,如果最后值大于等于K小于N则加入获胜总概率。时间复杂度较高。
1 | from collections import deque |
DP
使用上面两者暴力搜索方法当然不是最优的解法,因为其中包含了大量的重复计算,如果我们能够保存当前计算的状态,则可以大大降低时间复杂度。因此想到了DP动态规划。在这里我直接使用官方题解中的图片来阐述。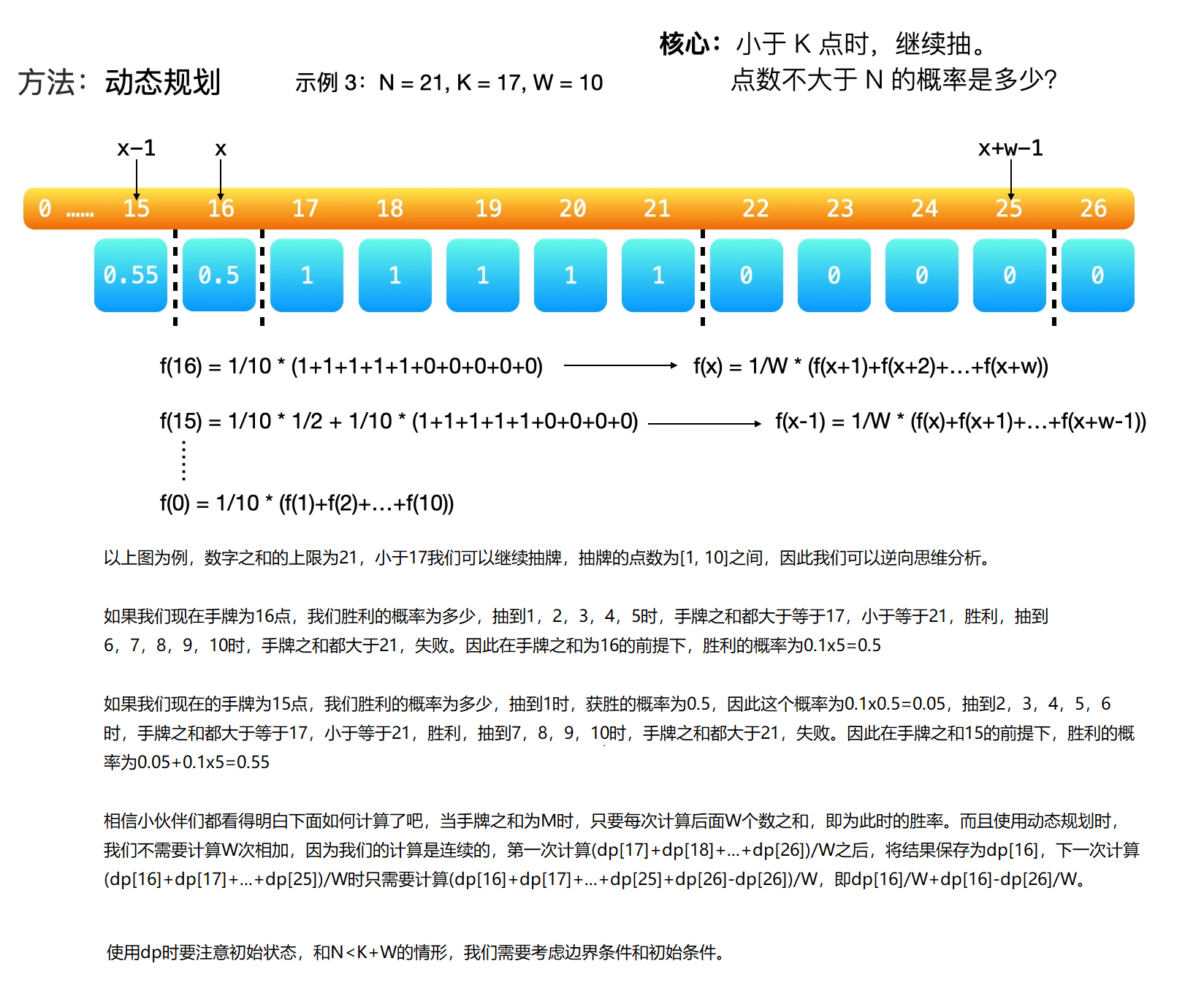
使用动态规划算法的时间复杂度为$O(min(N,K+W))$,空间复杂度为$O(K+W)$。
1 | class Solution: |
刷题总结
动态规划问题是面试时最常问的算法之一,因此这道题目的关键是掌握DP算法,并且学习反向DP的思考过程。